李宏毅机器学习笔记,坚持每天一更.
Machine Learning
0-Introduction of Machine Learning
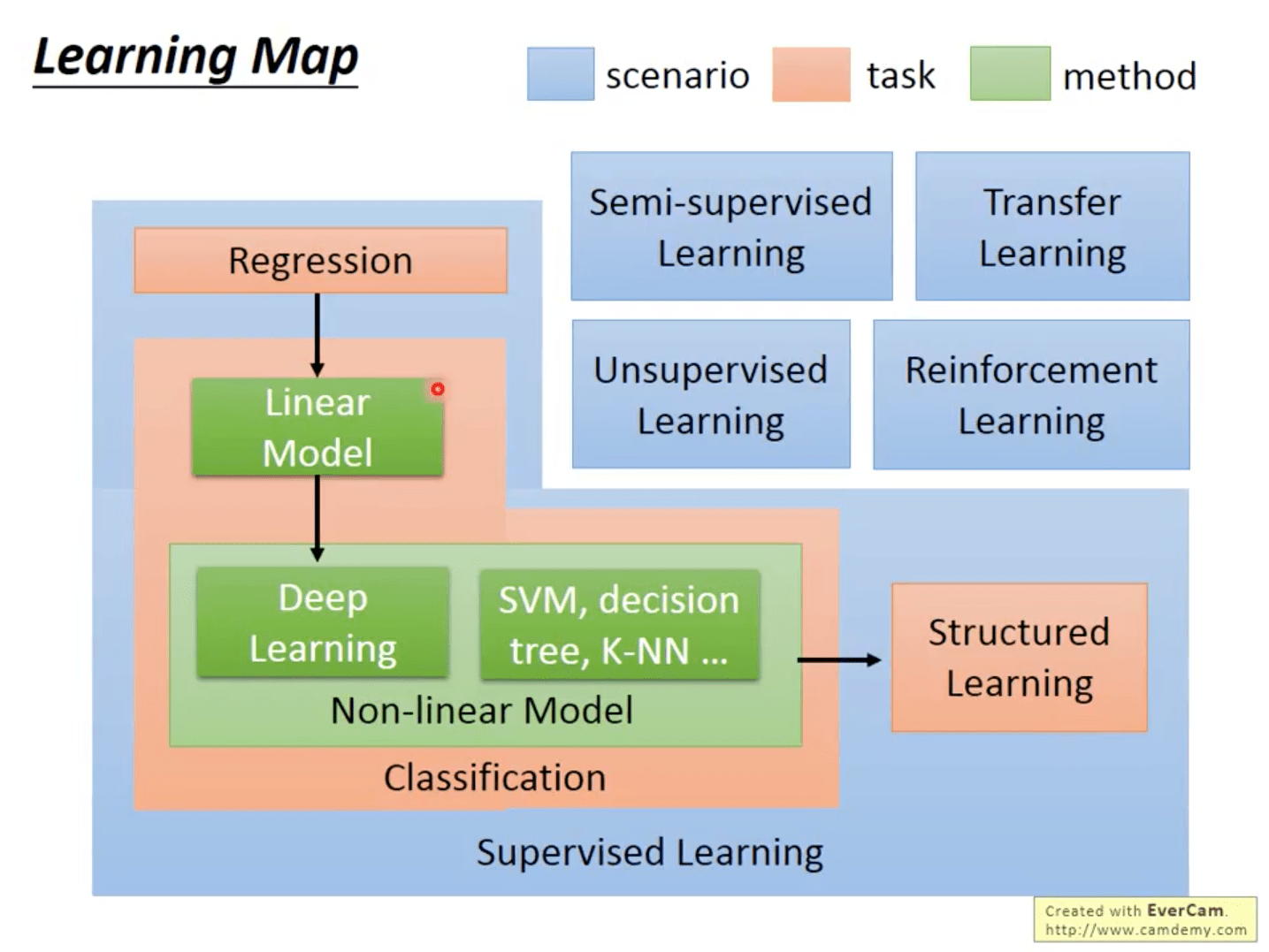
1-Regression
Application:
股票预测(Stock Market Forecast)
自动驾驶(Self-driving Car)
推荐系统(Recommendation)
Step1:Model
一堆函数:
$y = b + \sum w_{1,i} x_i + \sum w_{2,i} x_i^2 + … + \lambda \sum(w_i)^2$
总结:
其中$x_i$为某一项数据的第i个特征
$\sum(w_i)^2 $越小,函数越平滑
函数过于复杂,容易出现过拟合(Overfitting)的问题
Step2:Goodness of Function
损失函数 $L$:
输入: 一个函数
输出: 函数有多差
$L(f) = \sum_{i=1}^n (y_i - f(x_i))^2$
其中$y_i, f(x_i)$分别为第i项数据的真实y值与预测y值
Step3:Best Function
选取”最好”的函数: $f^*$
$f^* = arg min_f L(f)$
Gradient Descent
函数 $L(w)$ 只有一个参数 $w$时:
$w^* = arg min_w L(w)$
1.随机选取一个初始化的 $w^0$
2.计算微分 $w^1 = w^0 - \eta {dL \over dw}|_{w=w^0} $
3.计算微分 $w^2 = w^1 - \eta {dL \over dw}|_{w=w^1} $
.
.
.
经过多次迭代,计算出$w^*$
总结:
- 其中$\eta$为学习率(Learning rate)
- 经过梯度下降计算出来的最佳值可能是局部最小值(Local minima)和全局最小值(Global minima),”这个要看人品了”
- 当函数有多个参数时,求导过程变成求偏导的过程,每次迭代更新每个参数
两个参数的梯度下降过程示例:
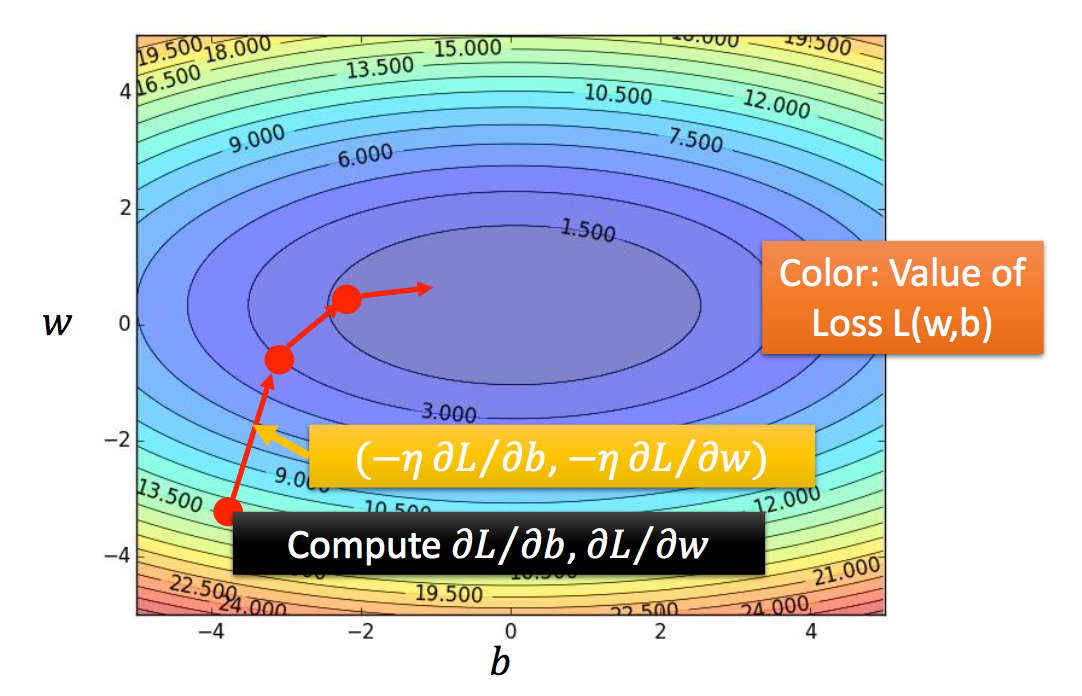
2-Bias and Variance(Where does the error come from)
错误来自偏差(bias)和方差(variance)
简单的模型偏差大、方差小,复杂的模型偏差小、方差
错误来自偏差说明模型欠拟合,错误来自方差说明模型过拟合
偏差指预测数据的均值与真实值的差值,方差描述预测数据的离散程度,如下图:
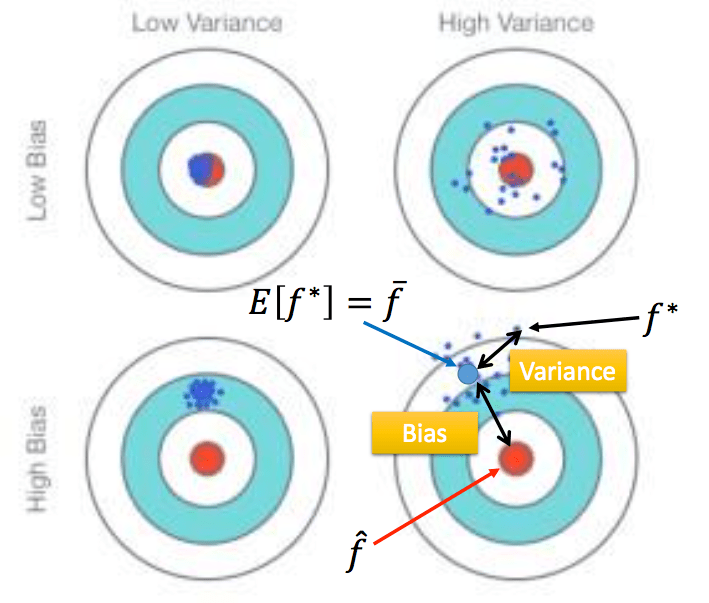
欠拟合:模型不能很好的拟合训练数据,拥有大的偏差
增加更多的特征,作为输入(Add more features as input)
选择更加复杂的模型(A more complex model)
过拟合:模型可以很好的拟合训练数据,但是在测试数据上表现很差,拥有大的方差
使用更多的数据来训练模型(More data)
正则化(Regularization)
Model Selection
选择模型时要考虑权衡上述两种错误因素,使得错误最小化
Cross Validation
可使用交叉验证的方法:交叉验证
3-Gradient Descent
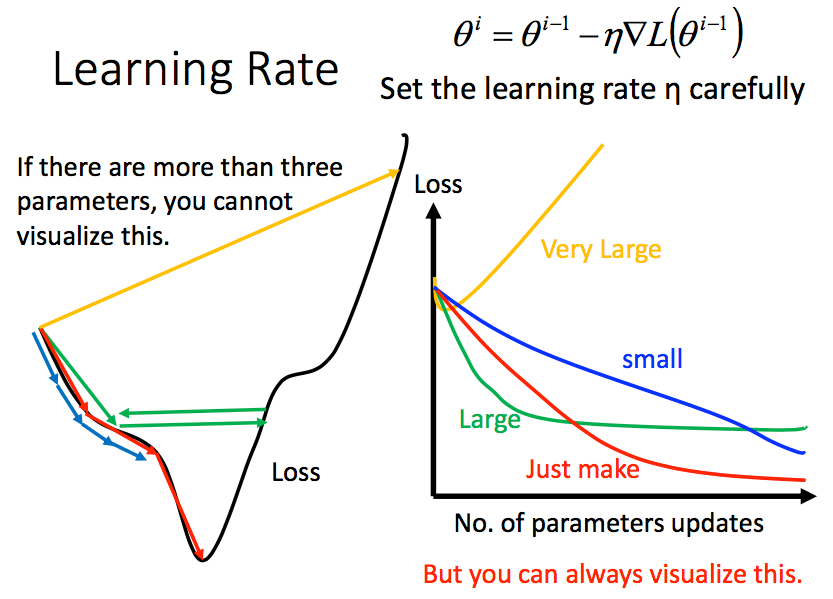
Tuning learning rate
$\theta^i = \theta^{i-1} - \eta {dL \over d\theta}|_{\theta=\theta^i} $
Set the learning rate η carefully
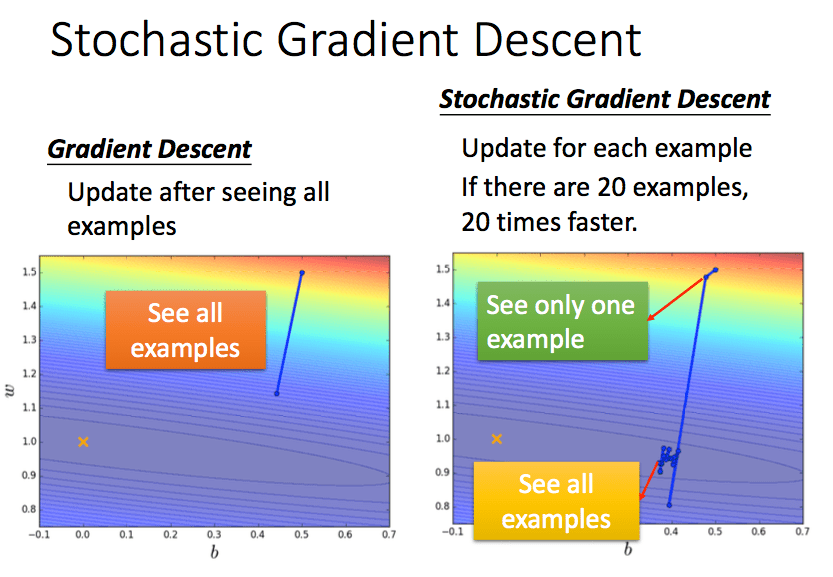
Stochastic Gradient Descent
随机梯度下降:每一个例子都更新一次参数
Feature Scaling
特征缩放属于数据标准化的范畴,能够消除每一维度特征对最后结果贡献的不平等性。(例如1,2,3,4,5…与100,200,300,400,500…)
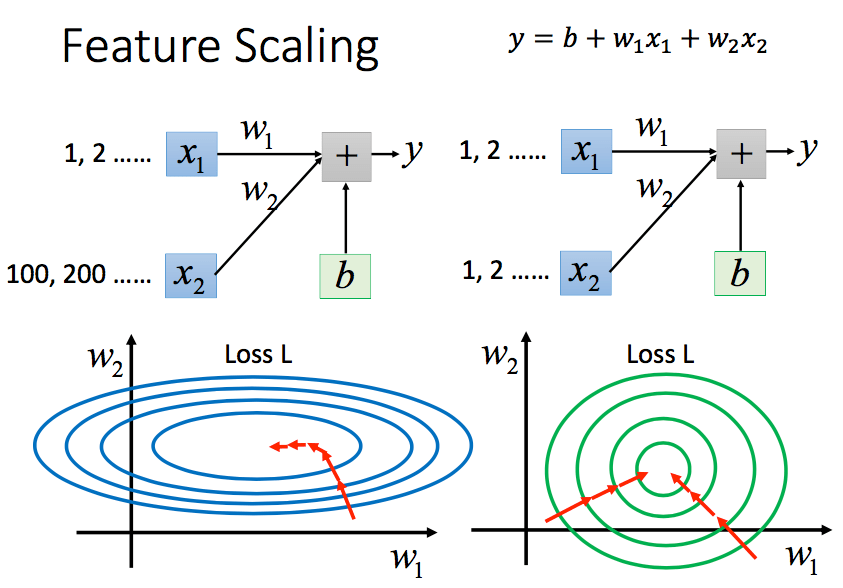
上图中$x_1$与$x_2$为不同特征
Gradient Descent Theory
利用泰勒展开式,近似求得

